Espelhos planos no periscóipio

Esta primeira atividade é para o aluno constatar as leis da reflexão.
Para isso faremos um experimento simples.

1) Uma pequena bola;
2) Giz;
3) Régua e transferidor de ângulos.

Como na figura abaixo, o professor traça no chão da sala de aula o ângulo de incidência (60°, por exemplo), a reta normal e o ângulo de reflexão (igual ao ângulo de incidência). Para isso o professor terá que utilizar os instrumentos de desenho geométrico. É um bom momento para se comentar a construção que foi feita. Depois peça para alguns alunos lançarem a bolinha procurando impor uma trajetória sobre o raio de incidência desenhado no chão. Todos devem observar a trajetória da bolinha depois da mesma se chocar com a parede.
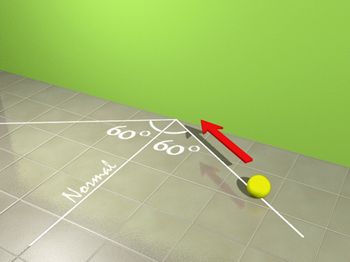
ilustração do autor
O professor pode alterar os ângulos para todos perceberem que a 2ª lei da reflexão sempre funcionará.

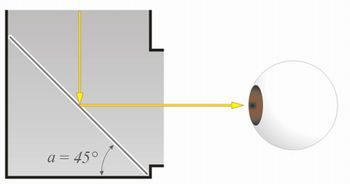
Esta segunda atividade é onde abordaremos a geometria do periscópio. Proponha o seguinte problema. Como poderemos visualizar a maçã da figura abaixo? O professor deve explicar que as setas amarelas compõem a trajetória de um raio de luz refletido da maçã até chegar aos olhos do observador. Os alunos certamente perceberão a necessidade do uso de espelhos na solução desse problema.
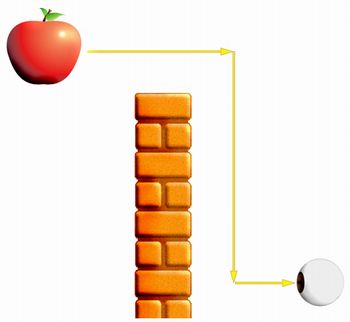
ilustração do autor
Neste momento o professor deve descrever o uso do periscópio neste tipo de problema e exibir o vídeo abaixo:
Acesse o vídeo em: (http://www.youtube.com/watch?v=5djO85vB93w)
Em seguida proponha o desafio:
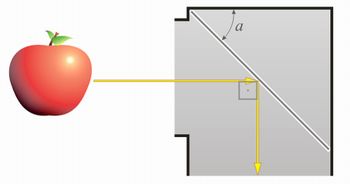
Observando a figura abaixo, que representa a parte de cima (objetiva) de um periscópio, determine o ângulo a, levando em conta as leis da reflexão.
ilustração do autor
Veja a evolução da solução:
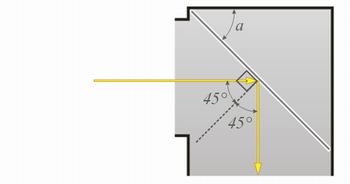
ilustração do autor
De acordo com a 2ª lei da reflexão os ângulos de incidência e de reflexão são iguais. Como a trajetória do raio de luz faz um ângulo reto, podemos concluir que os ângulos de incidência e reflexão valem 45°.
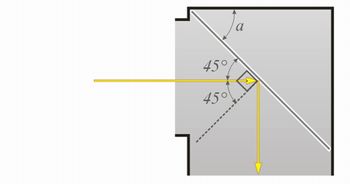
ilustração do autor
Sabemos que a reta normal é perpendicular ao plano do espelho. Como o ângulo de incidência é 45°, podemos afirmar que o ângulo entre o raio incidente e o espelho, também será de 45°.
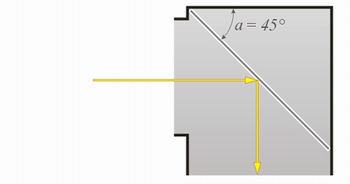
ilustração do autor
Como o raio incidente considerado é paralelo a base do periscópio, o ângulo entre o raio incidente e o espelho e o ângulo a são alternos internos, portanto iguais. Logo a = 45°.
ilustração do autor
Analogamente, podemos afirmar que o mesmo acontece na parte de baixo (ocular) do periscópio.
Discuta com os alunos os argumentos que eles usaram para se chegar ao ângulo de 45°.

Que tal construirmos os nossos próprios periscópios? É o que proponho nesta terceira atividade para ser feita em grupos.

- Uma folha de cartolina de boa consistência ou papel cartão na cor preta (o papelão pintado de preto também é uma boa opção);
- Dois espelhos de 6 cm x 9 cm;
- Cola;
- Esparadrapo.

Peça para os grupos desenharem e recortarem o corpo do periscópio conforme a figura:
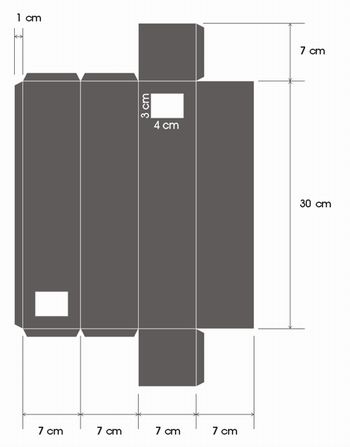
ilustração do autor
Agora peça para que os alunos façam a seguinte reflexão. Se a base do periscópio é 7 cm x 7 cm, quando deve medir x e y na figura abaixo?
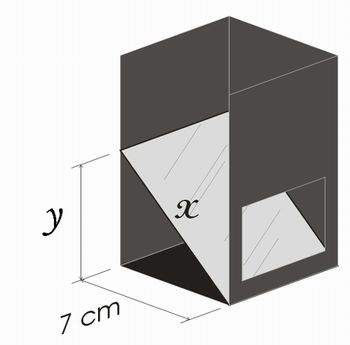
ilustração do autor
É hora de montar o periscópio. Dobre e cole a parte principal do corpo, mas deixe a "tampa" aberta para que seja possível prender os espelhos.
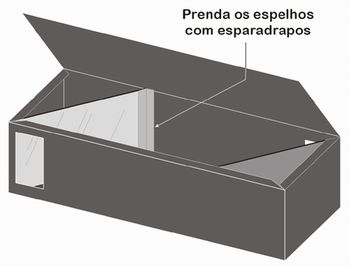
ilustração do autor
Prenda com esparadrapos e cole a tampa. O periscópio está pronto. Agora é só testá-lo pela escola.
Esta atividade foi extraída da aula Espelhos planos no periscópio, do professor Guilherme Erwin Hartung - Petrópolis/RJ Disponível no Portal do Professor/ MEC. Acessado em 12/07/2013. Todas as informações contidas são de responsabilidade do autor.